POP元件GLSL编写 -吸引子力场-TouchDesigner互动艺术空间

GLSL代码讲解（不用看懂是什么，只需要看懂有什么，）

// --- Uniforms: 从 TouchDesigner 传入的控制参数 ---

uniform float fa;               // uniform: 定义一个浮点数变量 fa (Force Amount)，用于整体缩放最终的力的大小。
uniform float falloff;          // uniform: 定义一个浮点数变量 falloff，用于控制力的衰减指数。
uniform float maxRadius;        // uniform: 定义一个浮点数变量 maxRadius (最大半径)，在此代码中未被使用。
uniform int normlaizeSum;     // uniform: 定义一个整数变量 normlaizeSum (应为normalizeSum)，在此代码中未被使用。

// --- 常量定义 ---

const float EPS = 1e-9;           // const: 定义一个极小的浮点数常量 EPS (Epsilon)，用于防止计算中出现除以零的错误。

// --- 主函数入口 ---

void main() {                     // main(): 所有 GLSL 程序的入口点，代码从这里开始执行。
    const uint id = TDIndex();      // TDIndex(): 获取当前正在处理的粒子/线程的唯一索引号 (ID)。
    
	// 这是一个安全检查，确保 id 没有超出处理范围
    if (id >= TDNumElements()) {    // TDNumElements(): 获取输入数据点的总数。
        return;                     // return: 如果 id 超出范围，则提前退出，不执行后续代码。
    }
        
    // --- 数据读取和初始化 ---
    
    vec3 pos = TDIn_P(0, id);       // TDIn_P(0, id): 从第 0 个输入源读取索引为 id 的点的位置(Position)。
    vec3 F = vec3(0.0);             // vec3(0.0): 创建一个三维向量 F (Force)，并初始化为零向量 (0,0,0)，用于累加所有的力。
    float totalw = 0.0;             // 创建一个浮点数 totalw (total weight)，用于累加权重，在此代码中未被使用。
    uint na = TDInputNumPoints(1);  // TDInputNumPoints(1): 获取第 1 个输入源（通常是吸引子）的总点数。

    // --- 循环计算 ---
    
    // 开始一个 for 循环，它将遍历第 1 个输入源中的每一个点（每一个吸引子）
    for (uint j = 0; j < na; j++) {
        
        // --- 向量和距离计算 ---
        
        vec3 aPos = TDIn_P(1, j);       // TDIn_P(1, j): 在循环中，获取当前吸引子的位置。
        vec3 d = aPos - pos;            // 向量减法: 计算出从当前粒子 (pos) 指向吸引子 (aPos) 的方向向量 d。
        float r2 = dot(d, d) + EPS;     // dot(d, d): 计算向量 d 的点积，结果是其长度的平方 (r²)，这比直接算长度更高效。
        float r = sqrt(r2);             // sqrt(r2): 对长度的平方进行开方，得到粒子到吸引子的精确距离 r。
        vec3 dir = d / r;               // 向量除法: 将方向向量 d 除以它的长度 r，得到一个长度为 1 的单位方向向量 dir (归一化)。
        
        // --- 权重和衰减计算 ---
        
        float w = 1.0;                  // 定义一个权重 w (weight)，这里设为常数 1.0。
        
        // 使用三元运算符判断如何计算力的强度 f (factor)
        // 如果 falloff > 0，则力的强度按 r 的 -falloff 次幂进行衰减 (距离越远，力越小)
        // 否则，力的强度恒为 1.0 (没有衰减)
        float f = (falloff > 0.0) ? pow(r, -falloff) : 1.0;

        // --- 累加总力 ---
        
        // 将方向(dir)、权重(w)和强度(f)相乘，得到来自当前吸引子的力向量...
        // ...然后使用 += 将这个力累加到总的力 F 上。
        F += dir * (w * f);
        totalw += w;                    // 将当前权重累加到总权重上 (在此代码中，结果未被使用)。

    } // for 循环结束

    // --- 输出最终结果 ---
    
    // 将累加后的总力 F 乘以总的缩放因子 fa...
    // ...然后将最终结果写入到输出 Buffer (名为 force) 中对应 id 的位置。
    force[id] = F * fa;
    
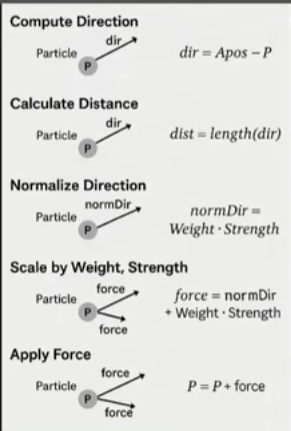
} // main() 函数结束

想象一下，你是个“上帝”，正在电脑里创造一个小世界。你的世界里有一个小球（粒子 P），还有一个神奇的磁铁（目标点 Apos）。你希望这个小球能被磁铁吸过去。这张图讲的就是你（作为上帝）在幕后需要进行的计算步骤，让小球知道该怎么飞。

咱们一步一步来看：

第1步：计算方向 (Compute Direction)

图中公式: dir = Apos - P
大白话讲解:
- 首先，小球得知道磁铁在哪边吧？它得有个方向感。
- 怎么算呢？很简单，用“终点”减去“起点”。你想让小球从 P 点飞到 Apos 点，那 Apos 就是终点，P 就是起点。
- Apos - P 就算出了一个箭头（在数学里叫“向量”），这个箭头正好从你现在的位置 (P) 指向你想去的地方 (Apos)。我们给这个箭头起个名字，叫 dir (Direction 的缩写)。
- 一句话比喻： 就像你在十字路口问路，别人给你指了个方向：“往那边走！”。这个“方向箭头”就是 dir。

第2步：计算距离 (Calculate Distance)

图中公式: dist = length(dir)
大白话讲解:
- 光知道方向还不够，小球还得知道自己离磁铁有多远。是近在咫尺，还是一眼望不到头？
- 上一步我们不是算出了那个叫 dir 的箭头吗？这个箭头的长度，不就是小球到磁铁的直线距离嘛！
- length() 是一个专门算箭头长度的“工具”（函数）。把 dir 扔进去，它就告诉你一个数字，这个数字就是距离 dist。
- 一句话比喻： 问路之后，你又问了一句：“那具体有多远啊？” 别人告诉你：“大概500米”。这个“500米”就是 dist。

第3步：归一化方向 (Normalize Direction)

图中公式: normDir = normalize(dir) (注意：图里原来的公式 Weight · Strength 是不对的，这里用正确的概念解释)
大白话讲解:
- 这是最关键也最不好理解的一步，但别怕。
- 上一步我们知道了距离，比如500米。但现在，我们想暂时忽略距离，只关心那个纯粹的“方向”。我们需要一个“标准的方向箭头”。
- “归一化” (Normalize) 就是把 dir 这个箭头的长度强行变成 1，但箭头指向的方向保持不变。我们管这个长度为1的“标准方向箭头”叫 normDir (Normalized Direction)。
- 为什么要这么干？因为这样一来，normDir 就成了一个万能的“方向舵”。以后我们想让力大一点，就在这个“方向舵”上乘以一个大数；想让力小一点，就乘以一个小数。它的作用就是只提供方向，力的大小由我们后面再决定。
- 一句话比喻： 你开车去一个地方，normDir 就好比是你的方向盘，它只管你车头朝哪，不管你油门踩多深。

第4步：调整力度 (Scale by Weight, Strength)

图中公式: force = normDir * Weight * Strength (同样，图里原来的 + 号是错的，应该是乘法)
大白话讲解:
- 现在我们有了标准的方向 (normDir)，该决定用多大的力气去推小球了。
- Weight (权重) 和 Strength (强度) 就是两个让你调节力大小的“旋钮”。
- 比如，你可以设定磁铁的吸引力强度 Strength 是 10。
- normDir (方向) 乘以 Strength (力度)，就得到了一个既有方向又有大小的“力” (Force)。这个 force 箭头，方向指向磁铁，长度就是10。
- 你还可以增加更多规则，比如“离得越近，吸力越强”，这就是 Weight 可以发挥作用的地方。
- 一句话比喻： 你已经把方向盘 (normDir) 摆正了，现在该决定踩多深的油门 (Strength) 了。方向盘和油门一结合，车子就获得了前进的动力 (force)。

第5步：施加力 (Apply Force)

图中公式: P = P + force
大白话讲解:
- 万事俱备！我们已经算出了一个完美的力 force。
- 现在就把这个力应用到小球身上。怎么用？非常简单，直接加起来！
- 用小球现在的位置 (P) 加上我们算出来的那个力 (force)，就得到了小球下一瞬间的新位置。
- 电脑会以极快的速度（比如每秒60次）重复这整个过程。每一次，小球的位置都会更新一点点，越来越靠近磁铁。连起来看，小球就像真的被吸过去一样，形成了一个平滑的动画。
- 一句话比喻： 你在A点，现在朝目标迈出了一步（这一步就是force），你就到达了一个新的点 A + 步长。持续不断地迈步，你就走到了终点。

总结

所以，这张图的整个故事就是：

一个小球，想去一个地方。它先抬头看准方向，估算一下距离，然后心里定好一个标准的前进方向。接着，根据需要决定这一步要迈多大，最后，迈出这一步。然后不断重复这个过程，直到到达目的地。

文章版权归作者所有，未经允许请勿转载。

THE END

未分类

POP元件GLSL编写 -吸引子 力场